Definição
Podemos fazer uso de tabelas, gráficos, e equações, como métodos para descrever como uma quantidade depende de outra. Esses métodos são ditos numéricos, visuais e algébricos.
Podemos fazer uso de tabelas, gráficos, e equações, como métodos para descrever como uma quantidade depende de outra. Esses métodos são ditos numéricos, visuais e algébricos.
O termo função foi usado por Leibniz em 1673 para descrever a dependência de uma quantidade de outra. Alguns exemplos desta situação são os seguintes:
“Se uma variável y depende de uma variável x, de tal forma que cada valor de x determina exatamente um valor de y, dizemos que y é uma função de x”. Podemos então definir função como:
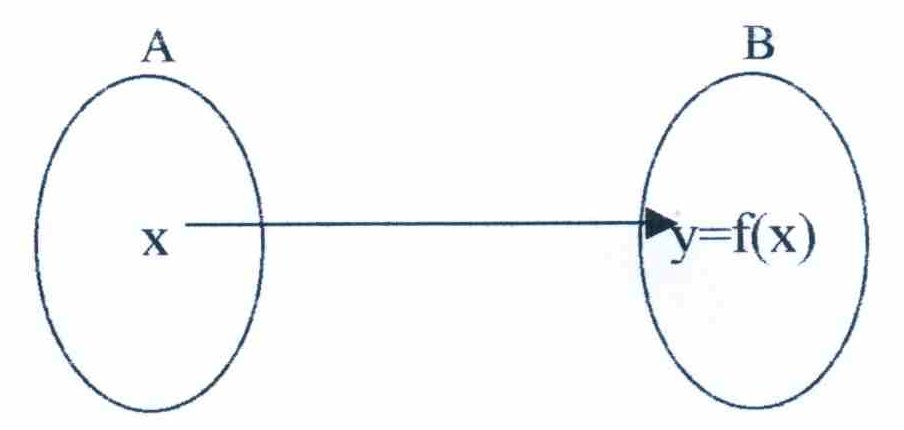
“Uma função f de um conjunto A num conjunto B é uma correspondência que associa a cada elemento x de A exatamente um elemento y de B”.
O elemento y de B é o valor de f em x e se denota por f(x) (lê-se f de x). O conjunto A é o domínio da função. A imagem de f é um subconjunto de B que consiste em todos os valores possíveis f(x) para x em A. B é chamado contradomínio de f.
- A área A de um de um quadrado depende do seu lado e é representada pela equação A= l2 assim, dizemos que A é uma função de r.
- A velocidade v de uma bola caindo livremente no campo gravitacional da Terra aumenta com tempo t que ela atinja o chão, assim dizemos que v é uma função de t.
- Em uma cultura, o número n de bactérias presentes após 1 hora de crescimento depende do número n0 de bactérias inicialmente presentes, assim dizemos que n é uma função de n0.
- Em uma certa empresa, o custo total de fabricação C depende do número de unidades produzidas q, assim dizemos C é uma função de q.
“Se uma variável y depende de uma variável x, de tal forma que cada valor de x determina exatamente um valor de y, dizemos que y é uma função de x”. Podemos então definir função como:
“Uma função f de um conjunto A num conjunto B é uma correspondência que associa a cada elemento x de A exatamente um elemento y de B”.
O elemento y de B é o valor de f em x e se denota por f(x) (lê-se f de x). O conjunto A é o domínio da função. A imagem de f é um subconjunto de B que consiste em todos os valores possíveis f(x) para x em A. B é chamado contradomínio de f.