Funçao Crescente
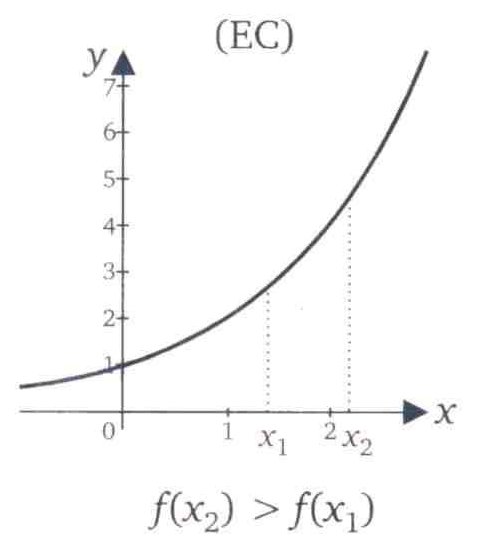
Seja f uma função definida em um conjunto A e sejam x1 e x2 dois pontos quaisquer de A, com x1 < x2 e sendo f(x1) < f(x2) dizemos que f é estritamente crescente em A.
É importante observar que se x1 < x2 e se f(x1) < = f(x2) a função é dita crescente.
Graficamente:
É importante observar que se x1 < x2 e se f(x1) < = f(x2) a função é dita crescente.
Graficamente:
Exemplificando:
Exemplo 1:
Seja a função definida em R e onde y = 2x –1. Esta é uma função estritamente crescente em seu domínio, pois dados dois números x1 e x2 com x1< x2 teremos:
Como x2 > x1, isto implica que x2 – x1 > 0 dessa forma f(x2) – f(x1) > 0 ou f(x2)> f(x1), o que permite comprovar que f é estritamente crescente em R. Como mostra o gráfico a seguir:
Exemplo 1:
Seja a função definida em R e onde y = 2x –1. Esta é uma função estritamente crescente em seu domínio, pois dados dois números x1 e x2 com x1< x2 teremos:
f(x2) – f(x1) = (2x2-1) – (2x1-1) = 2(x2 –x1)
Como x2 > x1, isto implica que x2 – x1 > 0 dessa forma f(x2) – f(x1) > 0 ou f(x2)> f(x1), o que permite comprovar que f é estritamente crescente em R. Como mostra o gráfico a seguir:

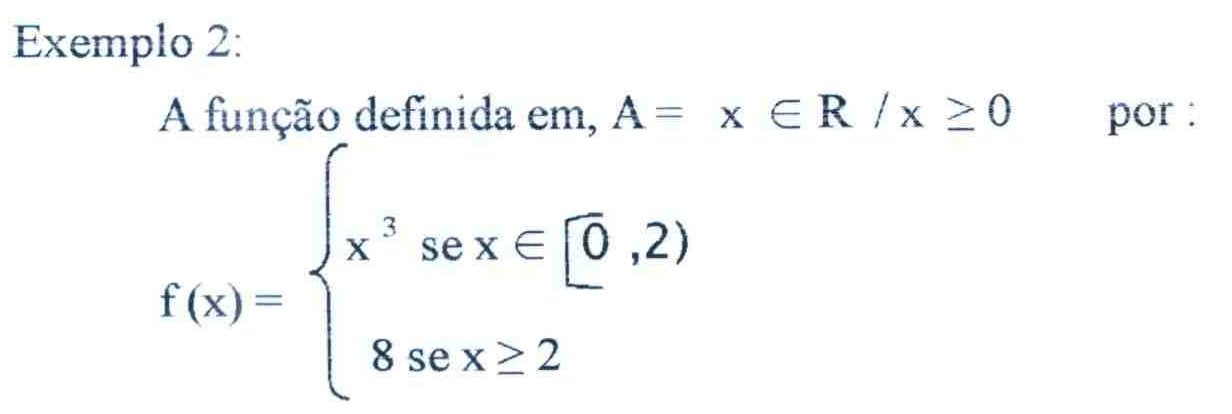
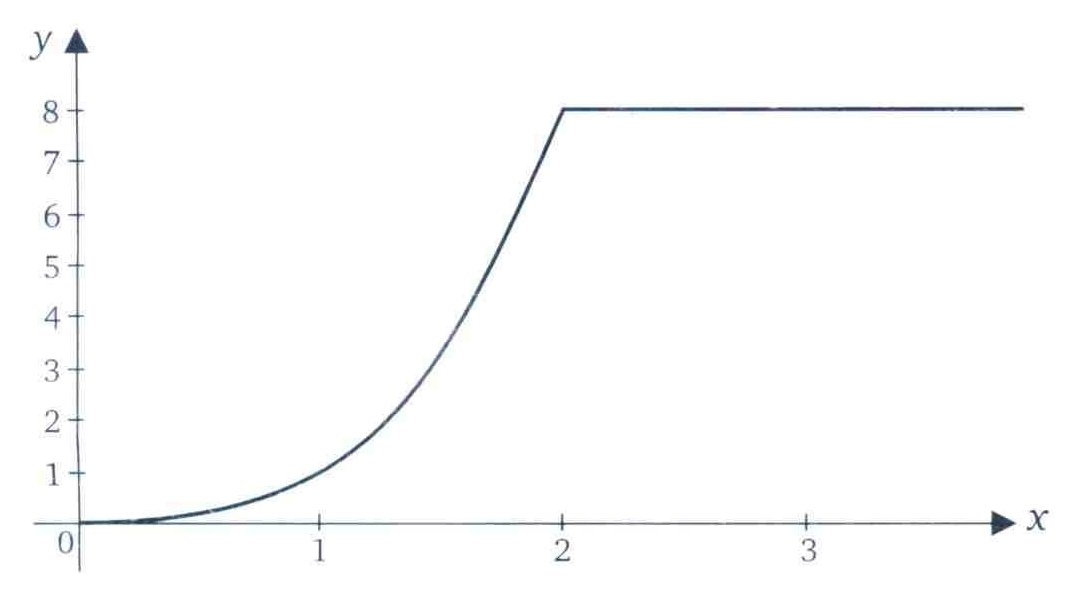
É uma função crescente em seu domínio, pois dados, dois pontos x1 e x2 de A como x2 > x1 teremos a seguinte situação :
Se 0 ≤ x1 < 2 então f(x2) - f(x1 ) = x23 – x13= (x2 – x1)(x23 + x13 – x2x1) = (x2 –x1) ((x2 – x1)x2 + x12) > 0, pois x2 – x1 > 0 e x2 > 0,ou seja f(x2)> f(x1)
Se x1≥ 2, então f(x2) = f(x1) = 8 o que implica que f(x2) = f(x1)
Resumindo, dados dois pontos x1 e x2 de A com x2 > x1, e f(x2) ≥ f(x1) a função é crescente no intervalo [0, + ∞) e cujo gráfico se encontra a seguir:
Se 0 ≤ x1 < 2 então f(x2) - f(x1 ) = x23 – x13= (x2 – x1)(x23 + x13 – x2x1) = (x2 –x1) ((x2 – x1)x2 + x12) > 0, pois x2 – x1 > 0 e x2 > 0,ou seja f(x2)> f(x1)
Se x1≥ 2, então f(x2) = f(x1) = 8 o que implica que f(x2) = f(x1)
Resumindo, dados dois pontos x1 e x2 de A com x2 > x1, e f(x2) ≥ f(x1) a função é crescente no intervalo [0, + ∞) e cujo gráfico se encontra a seguir: