Funçao Decrescente
Seja f uma função definida em um conjunto A e sejam x1 e x2 dois pontos quaisquer de A com x2 > x1. Então se f(x2) < f(x1) dizemos que f é estritamente decrescente em A.
Graficamente:

Devemos observar que se f(x2) ≤ f(x1) a função é dita decrescente em A. Podemos observar isto através da representação grafica:
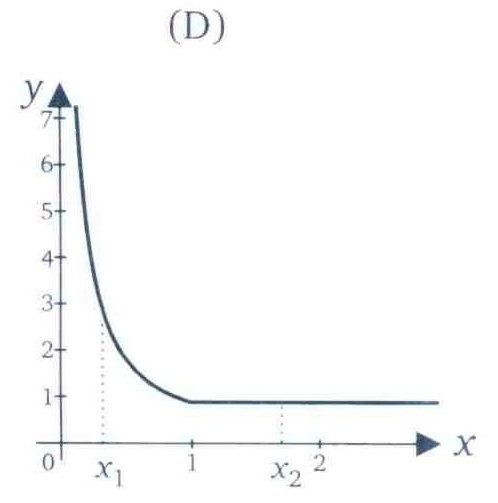
Exemplo :
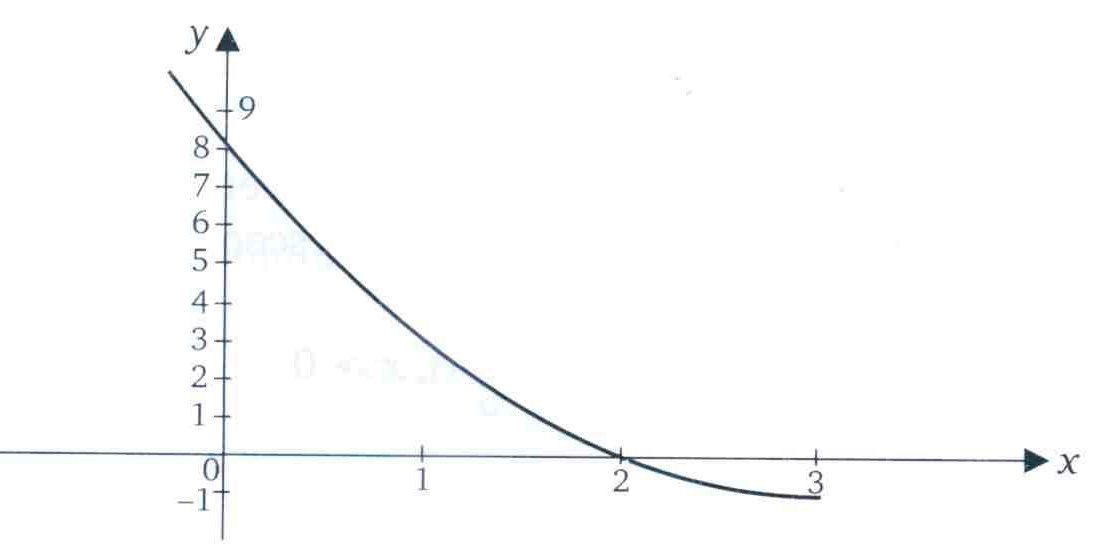
A função definida em R e tal que x^2 – 6x + 8 é estritamente decrescente no intervalo (-∞ ,3 ], pois, dados dois pontos x1 e x2 desse intervalo com x2 >x1 podemos escrever :
Como x2 > x1 ocorrerá x2 – x1>0. De outra forma, como x1< x2≤ 3 então x2 + x1-6< 0. Ou seja:
Através do gráfico temos:
A função definida em R e tal que x^2 – 6x + 8 é estritamente decrescente no intervalo (-∞ ,3 ], pois, dados dois pontos x1 e x2 desse intervalo com x2 >x1 podemos escrever :
f(x2) – f(x1) = (x2^2 –6x2 +8) – (x1^2- 6x1 +8) = x2^2 – x1^2 –6(x2-x1) = ( x2 – x1)(x2 + x1-6)
Como x2 > x1 ocorrerá x2 – x1>0. De outra forma, como x1< x2≤ 3 então x2 + x1-6< 0. Ou seja:
f(x2) –f (x1) < 0 ou f (x2) < f(x1).
Através do gráfico temos: