Função Linear

É uma função dada pela regra y = ax, com a  diferente de zero. Seu domínio é o conjunto dos Números Reais R. A representação gráfica da função linear é uma reta que contém a origem (0, 0) do sistema cartesiano, e o ponto (1, a).

A constante a é chamada coeficiente angular da reta e seu valor determina a inclinação da reta em relação ao sistema cartesiano.

Se a = 1, a regra da função linear passa a ser y = x e a função fica identificada como Função Identidade.

Exemplo:

1. y = x

Outro exemplo:

Seja y = 3x  e tendo como domínio o conjunto R dos números reais.




Função Linear Afim

É a função dada por y = ax + b, onde a e b são números reais não nulos. Seu domínio é o conjunto dos Números Reais. A representação gráfica desta função é uma reta que passa pelos pontos P1 = (0, b) e P2 = (1,a + b).

A constante a é o coeficiente angular, como na função linear e caracteriza a inclinação da reta. A constante b é o coeficiente linear e mede a altura do cruzamento da reta com o eixo oy.

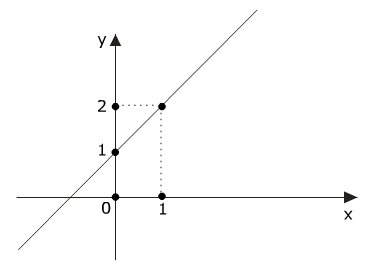
Exemplo:

1. y = x + 1

Outro exemplo:

Sendo y = -4x + 8 e tendo como domínio o conjunto dos números reais R.